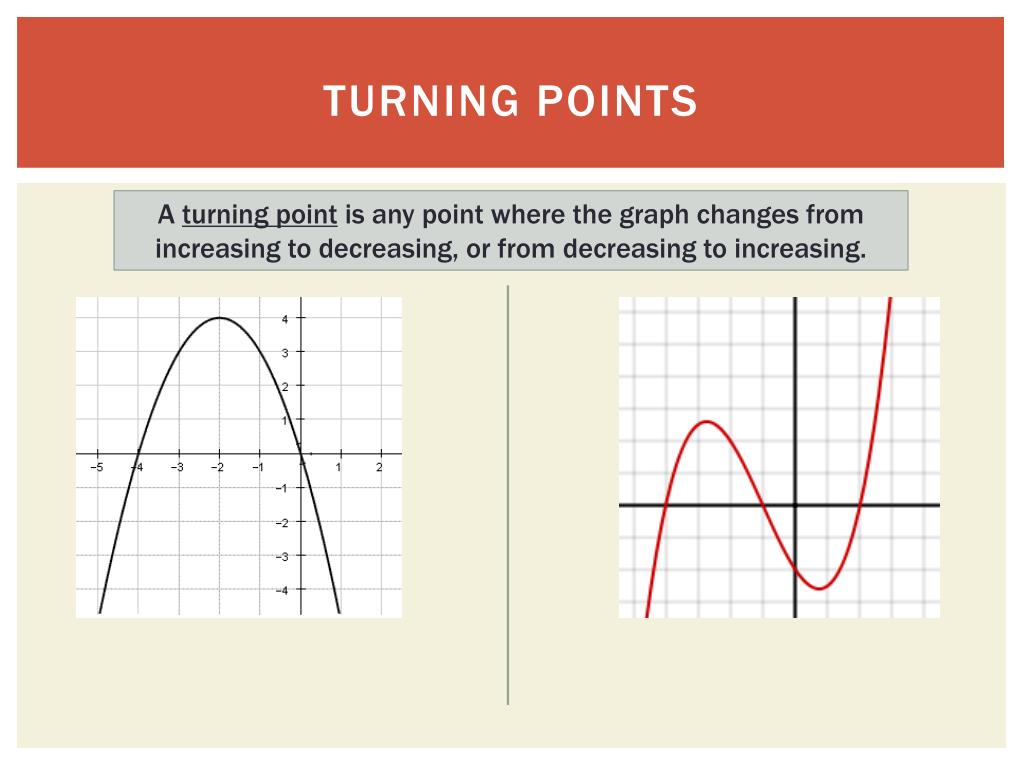
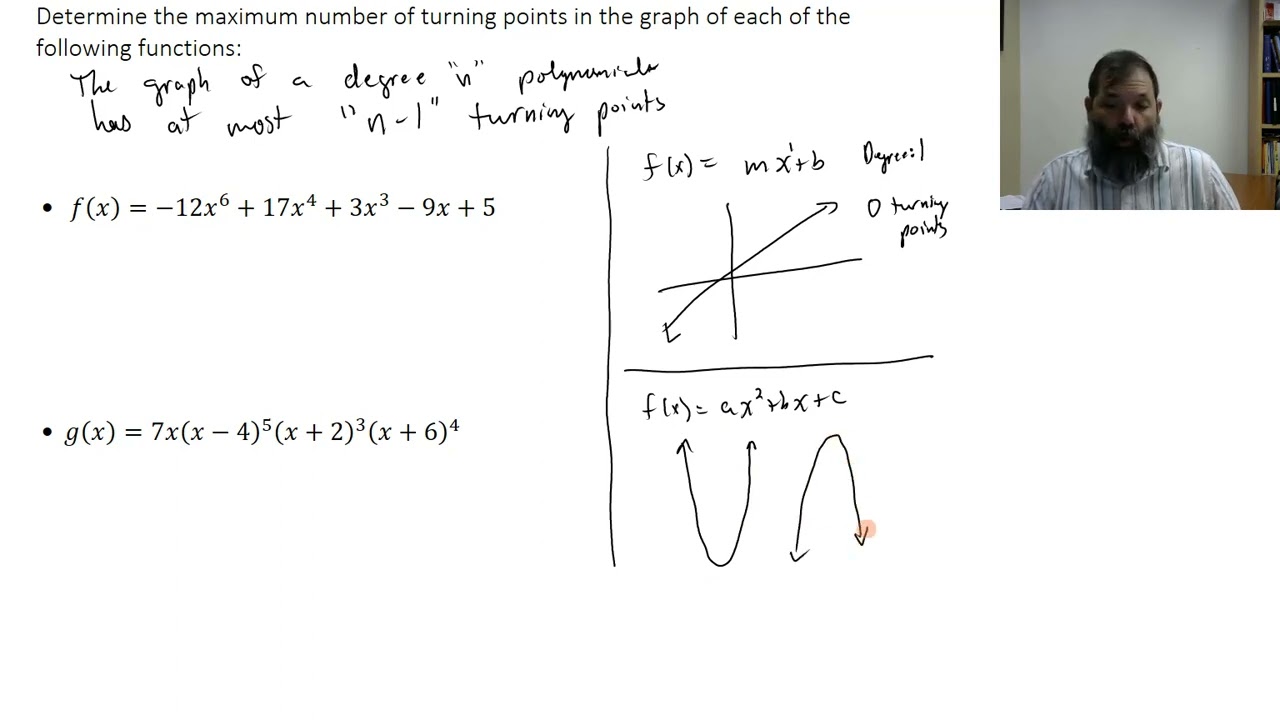
Number Of Turning Points - Figure 11 this function f is a 4 th degree polynomial function and has 3 turning points. The graph has three turning points. This is hard to understand: Demonstrates the relationship between the turnings, or bumps, on a graph and the degree of the associated polynomial. The number of turning points positives (and negatives) is odd. on reflection, i think you mean that the.
Demonstrates the relationship between the turnings, or bumps, on a graph and the degree of the associated polynomial. The graph has three turning points. The number of turning points positives (and negatives) is odd. on reflection, i think you mean that the. Figure 11 this function f is a 4 th degree polynomial function and has 3 turning points. This is hard to understand:
This is hard to understand: The number of turning points positives (and negatives) is odd. on reflection, i think you mean that the. The graph has three turning points. Figure 11 this function f is a 4 th degree polynomial function and has 3 turning points. Demonstrates the relationship between the turnings, or bumps, on a graph and the degree of the associated polynomial.
Modeling with Polynomial Functions ppt download
The number of turning points positives (and negatives) is odd. on reflection, i think you mean that the. This is hard to understand: Figure 11 this function f is a 4 th degree polynomial function and has 3 turning points. Demonstrates the relationship between the turnings, or bumps, on a graph and the degree of the associated polynomial. The graph.
Copyright © Cengage Learning. All rights reserved. ppt download
The graph has three turning points. This is hard to understand: Figure 11 this function f is a 4 th degree polynomial function and has 3 turning points. Demonstrates the relationship between the turnings, or bumps, on a graph and the degree of the associated polynomial. The number of turning points positives (and negatives) is odd. on reflection, i think.
How to Describe a Turning Point
Demonstrates the relationship between the turnings, or bumps, on a graph and the degree of the associated polynomial. Figure 11 this function f is a 4 th degree polynomial function and has 3 turning points. The number of turning points positives (and negatives) is odd. on reflection, i think you mean that the. This is hard to understand: The graph.
PPT Polynomial Functions PowerPoint Presentation, free download ID
The graph has three turning points. This is hard to understand: Figure 11 this function f is a 4 th degree polynomial function and has 3 turning points. The number of turning points positives (and negatives) is odd. on reflection, i think you mean that the. Demonstrates the relationship between the turnings, or bumps, on a graph and the degree.
[Solved] Determine the number of turning points of this polynomial
The number of turning points positives (and negatives) is odd. on reflection, i think you mean that the. The graph has three turning points. Figure 11 this function f is a 4 th degree polynomial function and has 3 turning points. This is hard to understand: Demonstrates the relationship between the turnings, or bumps, on a graph and the degree.
Analyze graphs of Polynomial Functions Lesson ppt download
This is hard to understand: The number of turning points positives (and negatives) is odd. on reflection, i think you mean that the. Demonstrates the relationship between the turnings, or bumps, on a graph and the degree of the associated polynomial. The graph has three turning points. Figure 11 this function f is a 4 th degree polynomial function and.
PPT Polynomial functions PowerPoint Presentation, free download ID
The number of turning points positives (and negatives) is odd. on reflection, i think you mean that the. Figure 11 this function f is a 4 th degree polynomial function and has 3 turning points. This is hard to understand: The graph has three turning points. Demonstrates the relationship between the turnings, or bumps, on a graph and the degree.
Assessment 3 Degree and Number of Turning Points of a Polynomial
This is hard to understand: Demonstrates the relationship between the turnings, or bumps, on a graph and the degree of the associated polynomial. The number of turning points positives (and negatives) is odd. on reflection, i think you mean that the. The graph has three turning points. Figure 11 this function f is a 4 th degree polynomial function and.
Determine maximum number of turning points for a polynomial function
Demonstrates the relationship between the turnings, or bumps, on a graph and the degree of the associated polynomial. The number of turning points positives (and negatives) is odd. on reflection, i think you mean that the. The graph has three turning points. Figure 11 this function f is a 4 th degree polynomial function and has 3 turning points. This.
Analyze graphs of Polynomial Functions Lesson ppt download
The number of turning points positives (and negatives) is odd. on reflection, i think you mean that the. Figure 11 this function f is a 4 th degree polynomial function and has 3 turning points. This is hard to understand: The graph has three turning points. Demonstrates the relationship between the turnings, or bumps, on a graph and the degree.
This Is Hard To Understand:
Figure 11 this function f is a 4 th degree polynomial function and has 3 turning points. The number of turning points positives (and negatives) is odd. on reflection, i think you mean that the. Demonstrates the relationship between the turnings, or bumps, on a graph and the degree of the associated polynomial. The graph has three turning points.